REPRESENTACIÓN DE LA DISTRIBUCIÓN DE LA PROBABILIDAD PARA LA VARIABLE ALEATORIA DISCRETA

REPRESENTACIÓN DE LA DISTRIBUCIÓN DE LA PROBABILIDAD PARA LA VARIABLE ALEATORIA DISCRETA.

Distribuciones discretas de probabilidad

Función de probabilidad

Se llama función de probabilidad de una variable aleatoria discreta X a la aplicación que asocia a cada valor de x_i de la variable su probabilidad p_i.

0 ≤ p_i ≤ 1

p₁ + p₂ + p₃ + · · · + p_n = Σ p_i = 1

Ejemplo

Calcular la distribución de probabilidad de las puntuaciones obtenidas al lanzar un dado.

x	p i
1
2
3
4
5
6
1

Representación

La representación de una distribución discreta de probabilidad es un diagrama de barras.

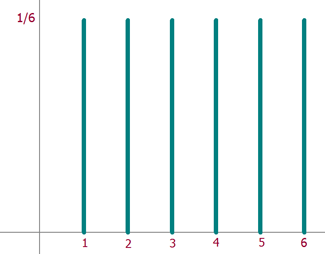
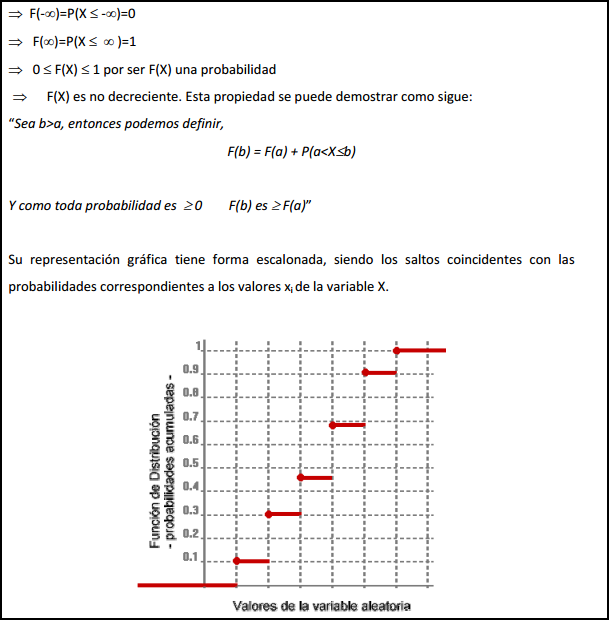
Función de distribución

Sea X una variable aleatoria discreta cuyos valores suponemos ordenados de menor a mayor. Llamaremos función de distribución de la variable X, y escribiremos F(x) a la función

F(x) = p(X ≤ x)

La función de distribución asocia a cada valor de la variable aleatoria la probabilidad acumulada hasta ese valor.

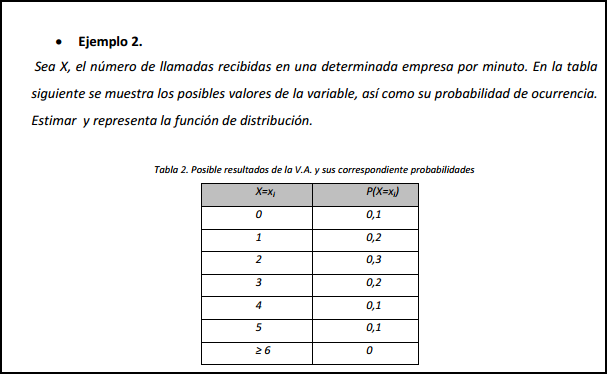
Ejemplo

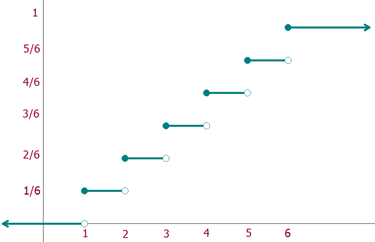
Calcular la función de distribución de probabilidad de las puntuaciones obtenidas al lanzar un dado.

x	p i
x <1	0
1≤ x < 2
2≤ x < 3
3≤ x < 4
4≤ x < 5
5≤ x < 6
6≤ x	1

Representación

La representación de un función de distribución de probabilidad es una gráfica escalonada.

Parámetros de una distribución de probabilidad

Media o esperanza matemática

La media de una distribución de probabilidad se denota por la letra griega µ (mu).

A la media también se le suele llamar valor esperado o esperanza matemática y se puede denotar como E(x).

Estos nombres tienen su origen en los juegos de azar y hacen referencia a la ganancia promedio esperada por un jugador cuando hace un gran número de apuestas.

Si la esperanza matemática es cero, E(x) = 0, el juego es equitativo, es decir, no existe ventaja ni para el jugador ni para la banca.

Varianza

La varianza y desviación típicade una distribución de probabilidad se denotan por la letra griega σ (sigma) : σ² y σ.

Desviación típica

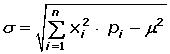
Ejemplo

Calcular la esperanza matemática, la varianza, y la desviación típica, de la distribución de probabilidad de las puntuaciones obtenidas al lanzar un dado.

x	p i	x· p i	x 2 ·pi
1
2
3
4
5
6		1	6

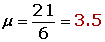
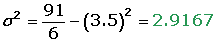
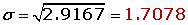
Tabla de distribución de frecuencias

La tabla de distribución de frecuencias muestra los resultados obtenidos

2.  Tabla de distribución de probabilidad

La tabla de distribución de probabilidad muestra los resultados esperados

3.  Gráfica de las distribuciones

En la gráfica de los valores esperados, observamos que a cada valor de la variables aleatoria xi "cara del dado" le hacemos corresponder su probabilidad teórica. A esta ley se le llama distribución de probabilidad.

Función y Distribución de Probabilidad.

La función de los valores numéricos de x la representamos por f(x), g(x), r(x), etc. y la probabilidad de que la variable aleatoria X tome el valor xcon P(X = x ).

Sean x₁, x₂, ..., x_n (espacio muestral de X), los valores para los cuales Xtiene probabilidad y sean p₁,  p₂ ,..., p_n  las probabilidades correspondientes. Entonces P(X = x₁) = p_1. Bajo este criterio podemos decir que:

Si 

a f(x_i) se le llama función de probabilidad.

La función de probabilidad debe satisfacer las siguientes propiedades:

1)    f(xi) ³ 0.

2)    S f(xi) = 1

A partir de la función de probabilidad podemos establecer el concepto de distribución de probabilidad en la forma siguiente:

La distribución de probabilidad de una variable aleatoria discreta se presenta como la lista de los distintos valores xi que puede tomar la variable aleatoria X, junto con sus probabilidades asociadas f(x_i) = P(X = x_i), esto es, el conjunto de parejas {x_i, f(x_i)}.

Ejemplo 4. 2. Sea X el número que se obtiene al arrojar un dado legal. Encontrar la distribución de probabilidad correspondiente.

Solución.

Los valores que puede tomar la variable aleatoria son 1, 2, 3, 4, 5, 6 y como el dado es legal, todos los valores tienen probabilidad 1/6. En consecuencia:

xi	1	2	3	4	5	6
f(xi)	1/6	1/6	1/6	1/6	1/6	1/6

Para representar gráficamente la distribución de probabilidad se usa un diagrama de líneas. Para construir este gráfico, los distintos valores de la variable aleatoria X se registran en el eje horizontal. En cada valor x_i se dibuja una línea vertical cuya altura es igual a la probabilidad correspondiente f(xi).

Dibujar gráfica de la distribución de probabilidad

Ejemplo 4. 3. Suponga que dos productos A y B de la misma calidad son comparados por cuatro personas, las cuales expresan su preferencia por A o por B. Sea X la variable aleatoria definida como el número de personas que prefieren el producto A. Encontrar la distribución de probabilidad.

Solución.

El espacio muestral correspondiente es:

S = {AAAA, AAAB, AABA, ABAA, BAAA, AABB, ABAB, ABBA, BAAB, BBAA, BABA, ABBB, ABBB, BBAB, BBBA, BBBB}

donde cada punto muestral es una sucesión de cuatro símbolos A o B.

Los elementos del espacio muestral (eventos simples), los podemos escribir en la forma siguiente:

AAAA             AAAB             AABB             ABBB             BBBB

                                   AABA             ABAB             BABB

                                    ABAA             ABBA             BBAB

                        BAAA             BAAB             BBBA

                                                           BBAA

                                                           BABA            

Supongamos que los consumidores expresan su preferencia en forma independiente. Como los productos son de igual calidad, los 16 puntos muestrales son igualmente posibles de ocurrir y tienen una probabilidad de 1/16.

Los eventos simples se han agrupado de tal forma que todos los eventos en una columna tengan el mismo valor para X = Número de personas que prefieren el producto A. Por ejemplo, para los eventos de latercer columna, X toma el valor de 2. Es decir:

X(AABB) = X(ABAB) = X(ABBA) = X(BAAB) = X(BBAA) =X(BABA) = 2

Sumando las probabilidades de los eventos simples a los que se les asigna el mismo valor de X, obtenemos los valores que se muestran en la tabla siguiente, la cual representa la distribución de probabilidad de la variable aleatoria X.

Xi	0	1	2	3	4
f(xi)	1/16	4/16	6/16	4/16	1/16

De la distribución de probabilidad podemos obtener todas las probabilidades que dependan de los valores que pueda tomar la variable aleatoria X. Por ejemplo:

P(X £ 2) = P(X = 0) + P(X = 1) + P(X = 2) = 1/16 + 4/16 + 6/16 = 11/16

P(1 £ X £ 3) = P(X = 1) + P(X = 2) + P(X = 3) = 4/16 +6/16 +4/16 = 14/16

P(X>2) = P(X = 3) + P(X = 4) = 4/16 + 1/16 = 5/16

Ejemplo 4. 4. Una tienda pone en venta de liquidación sus últimos 15 radios despertador. Se desconoce que 5 de estos radios están defectuosos. Un comprador selecciona al azar tres radios y los prueba. Sea X la variable aleatoria definida como el número de radios defectuosos entre los seleccionados. Construya la distribución de probabilidad de la variable aleatoria X.

Solución.

Como únicamente estamos interesados en el número de radios defectuosos entre los seleccionados, resulta irrelevante el orden en el cual se seleccionan los radios. Podemos calcular directamente las probabilidades para los diferentes valores de X, haciendo uso del concepto de combinaciones.

En este ejemplo no es necesario describir al espacio muestral para poder determinar los diferentes valores de la variable, ya que resulta evidente que el número de radios defectuosos en la muestra puede ser 0, 1, 2 ó 3, es decir: x_i= 0, 1, 2, 3.

Para el cálculo de las probabilidades utilizaremos el modelo matemático . Calculemos cada uno de los valores que se necesitan para obtener la distribución.

N será la magnitud del espacio muestral y en este caso corresponde al número de formas posibles en que se pueden seleccionar 3 radios despertador de los 15 que hay, por lo que:

Como de los 15 radios despertador 5 son defectuosos entonces 10 son buenos. X = 0 significa que dentro de los 3 radios despertador que se seleccionan ninguno es defectuoso, por lo que todos son buenos. En consecuencia:

X = 1 significa que dentro de los 3 radios despertador que se seleccionan uno es defectuoso, por lo que 2 son buenos y así se hace el análisis para los demás valores de x.

            La distribución de probabilidad del número de radios defectuosos se muestra en la tabla siguiente:

X = xi	0	1	2	3
f(xi)	120/455	225/455	100/455	10/455

            La forma de comprobar que las probabilidades calculadas son correctas, es comprobar que la suma de las mismas dé la unidad. Así, , lo cual indica que los valores son correctos.